Research areas of interest
| 1. Synthesis of nanoparticles |
| 2. Population balance equations (PBE) |
| 3. Monte-Carlo simulations |
| 4. Process Intensification |
| 5. Agitated Liq-Liq Dispersions |
| 6. Energy Storage |
1. Synthesis of nanoparticles
Nanoparticles find applications in a wide variety of fields. The efforts in our group (jointly with Prof. Venugopal) are focussed on developing engineering scale processes for synthesis of metal and inorganic nanoparticles. The route taken is to explore the relative role of various mechanisms, such as nucleation, growth, coagulation, capping, and ripening of nanoparticles in influencing particle size distribution, and ways to externally modulate these mechanisms to exercise the desired control on mean size and polydispersity. We use the framework of population balances to model nanoparticle synthesis.
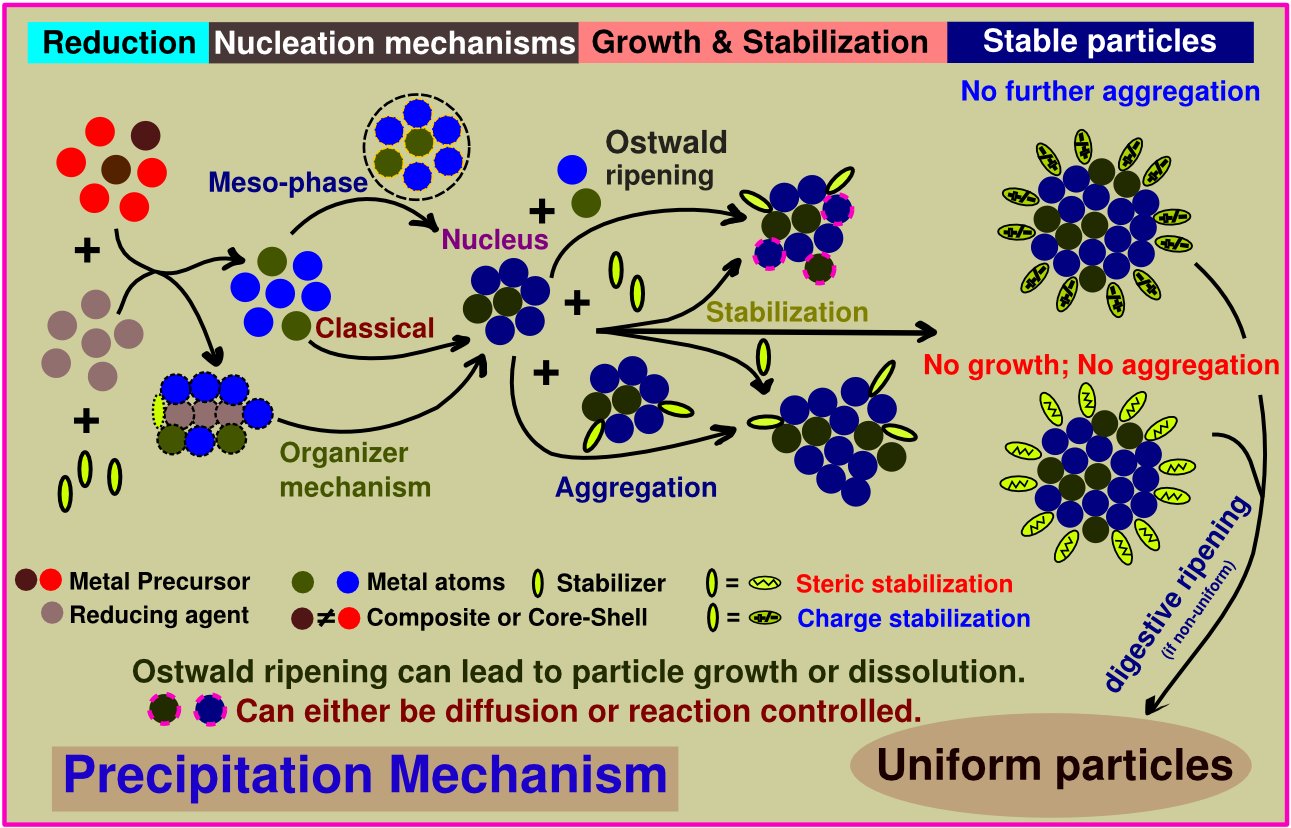
Different steps involved in the formation of nanoparticles
2. Population balance equations (PBEs) |
Back to top |
Population balance equations (PBEs) are similar to the widely used mass and energy balance equations. PBEs account for birth, growth, aggrgeation, breakup, and disappearance of particles. Particles can be bubbles, drops, nanoparticles, micelles, bacteria, polymers, viruses, etc. When a particle is identified with a single variable, such as its volume, 1-d PBE is obtained. If more than one internal attributes of particles need to be specified to identify particles uniquely, multi-dimensional PBEs are obtained. Our group has developed a set of discretization techniques to solve one and multi-dimensional PBEs, based on the frameworks of internal consistency and minimal internal consistency of discretization developed by us.
3. Monte-Carlo simulations |
The stochastic processes of particle birth, aggregation, and breakup are quite naturally simulated using Monte-Carlo simulation techniques. Although these techniques are ideally suited only for batch systems, they are quite useful as the programming effort required is minimum. Our group has recently developed novel methods to overcome their main shortcoming---computation intensive nature of simulation. One of these methods makes use of simulations carried out with extremely small size systems to construct system size independent results, that otherwise require (CPU intensive) simulations with large size systems.
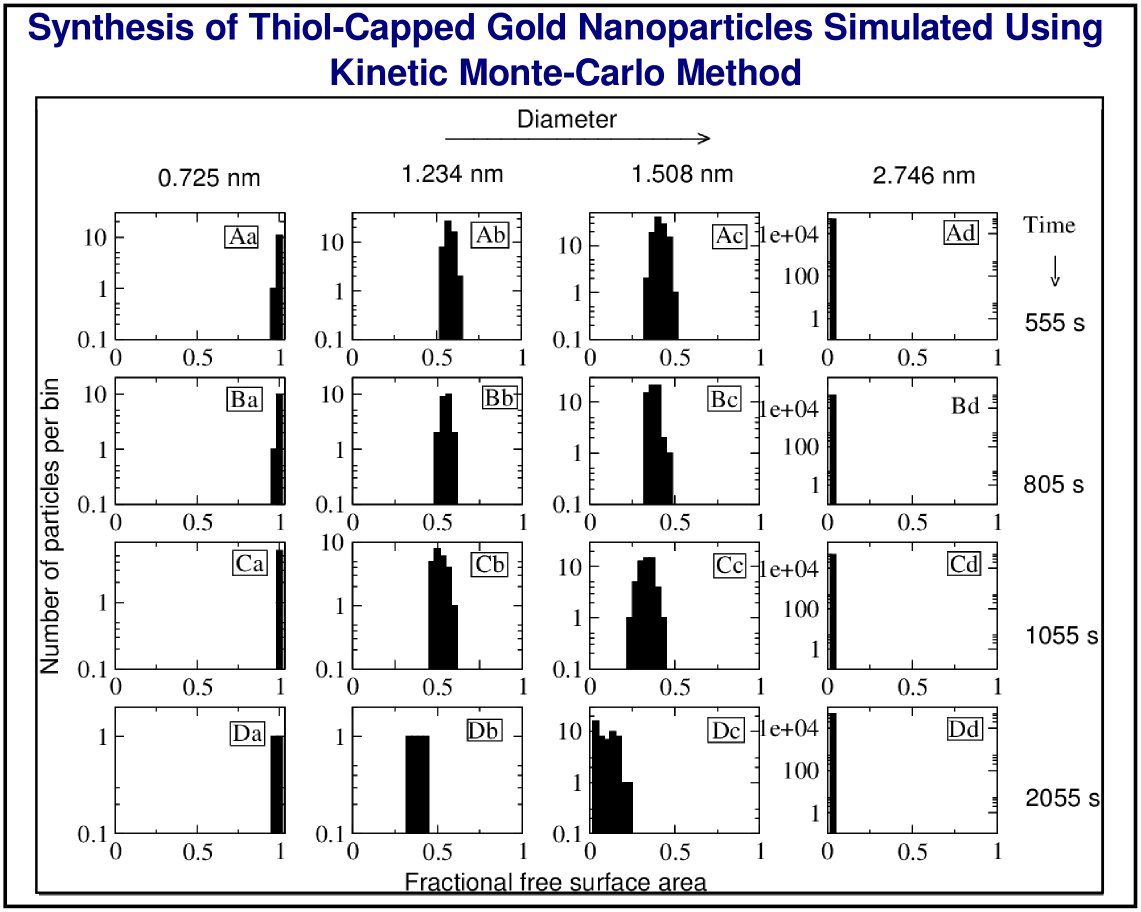
A kinetic Monte-Carlo solution of bivariate population balance equation (to simulate the synthesis of nanoparticles).
4. Process intensification |
5. Agitated Dispersions and Phase Inversion |
Agitated liquid-liquid dispersions are used to carry out liquid-liquid extraction, multi-phase reaction, direct contact heat transfer, etc. The prediction of dynamics of such processes requires an understanding of the basic processes of breakup and coalescence of drops, and the use of the framework of population balances to make use of the rate processes associated with them.
Our group has contributed significantly to the understanding of these processes, and continues to invest effort in understanding an interesting phenomena, named phase inversion. As the volume fraction of the dispersed phase is increased, at a critical value, the dispersed phase becomes the continuous phase and vice-versa. Our recent work has shown that phase inversion in sufficiently intense turbulence is independent of what means are employed to generate turbulence, and is a property of the liquid-liquid system. Our recent experimental findings suggest that dispersion goes through an interesting dynamic strcture close to the inversion point.
6. Electrochemical Energy Storage: Modeling of Batteries and Electrochemical Capacitors |
Back to top |
Given the increasing demand for clean energy, stringent laws for emission control and depleting reservoirs of fossil fuels, energy storage devices for solar energy, wind energy and transportation will play a critical role in modern life style. Applications include energy storage at electric grids, electric cars and high power electric tools. Devices with high energy density, long cycle life, higher rates of charge and discharge, and low cost of manufacture are desirable.
Our group has initiated efforts to understand and quantify the processes in Electrochemical systems such as Redox Flow Batteries (RFBs) and Electrochemical Capacitors (ECs).
We use Mathematical Modeling as a tool to investigate the systems and validate our understanding using Experiments to increase the cycle life of flow batteries and to improve the operating efficiency of ECs. As engineers, we are interested in understanding the system well enough to design for desired performance at lower cost.
We work on Soluble lead redox flow battery (SLRFB), Zinc-Cerium redox flow battery, Electrochemical Double Layer Capacitors and Hybrid Capacitors.