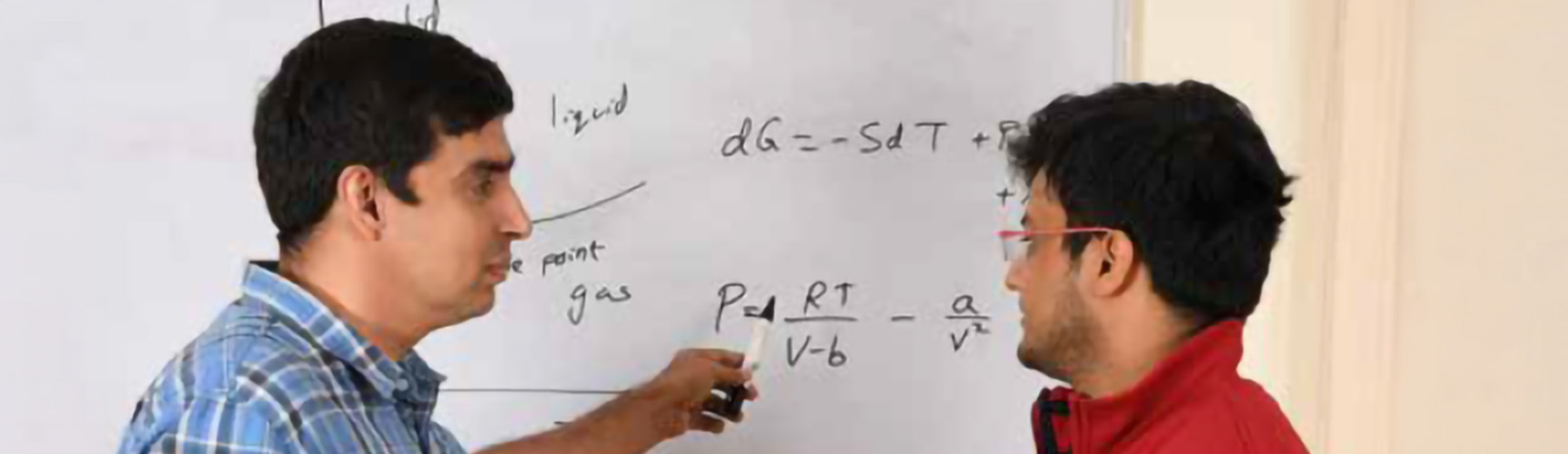

The actual courses offered for a semester along with instructor's names are available on IISc course registration portal via your SAP login.
Please visit the Chemical Engineering Intranet Page to find the latest courses and academic calendar.
CH 201 (AUG) 3:0 - Chemical Engineering Mathematics
Linear algebraic equations, linear operators, vector and function spaces, metric and normed spaces, existence and uniqueness of solutions. Eigen values and eigen vectors/functions. Similarity transformations, Jordan forms, application to linear ODEs, Sturm-Liouville problems. PDE’s and their classification, initial and boundary value problems, separation of variables, similarity solutions. Laplace and Fourier transforms.
CH 202 (AUG) 3:0 - Numerical Methods
Basics of scientific computing, numerical errors, solution of linear algebraic equations, linear least squares, eigen values, eigen vectors, solution of nonlinear equations, optimization methods, nonlinear least squares, interpolation, numerical differentiation and integration, solution of ODEs – initial and boundary value problems, finite differences for PDEs
CH 203 (AUG) 3:0 - Transport Processes
Basic transport laws and transport properties; shell and differential balances; Navier-Stokes equations, equations of change for temperature and concentration in dilute systems; similarity of three transport processes; steady and unsteady transport, forced and natural convection; convective diffusion in dilute solutions; integral balances and connection to unit operations; boundary layer theory, turbulence.
CH 204 (AUG) 3:0 - Thermodynamics
Classical thermodynamics: first and second laws, Legendre transforms, properties of pure substances and mixtures, equilibrium and stability, phase rule, phase diagrams, and equations of state, Calculation of VLE and LLE, Reaction equilibria, Introduction to statistical thermodynamics.
CH 205 (JAN) 3:0 - Chemical Reaction Engineering
The condition for reaction equilibrium; equilibrium constant and the equilibrium composition; degrees of freedom for reactive systems; rate expressions for reactions; theories for the rates of reactions; ideal and actual reactors. Mass and energy balances for an ideal batch reactor; application to the oxidation of lignin. The ideal continuous stirred tank reactor: mass and energy balances; steady state analysis; van Heerden’s graphical approach; stability of steady states; linearized stability analysis; The empty tubular reactor: cross-sectional averaged balances; parametric sensitivity and runaway behaviour; a bubble column slurry reactor for Fisher-Tropsch synthesis. The attainable region analysis for sequences of reactors. Diffusion and reaction in catalyst pellets; differential balances; flux relations; effectiveness factors; diffusional disguise of rate parameters; external resistances to heat and mass transfer. The packed bed catalytic reactor. Nonideal flow through reactors; residence time distribution; micromixing and macromixing.
CH 206 (AUG) 1:0 - Seminar Course
The course aims to help students in preparing, presenting and participating in seminars. The students will give seminars on topics chosen in consultation with the faculty.
CH 207 (JAN) 1:0 - Applied Statistics and Design of Experiments
Introduction to probability and statistics; conditional probability; independence; discrete and continuous random variables and distributions; sampling distributions; confidence interval; application of parameter 170 estimation and hypothesis testing: statistical inference for one sample and two samples; application of parameter estimation and hypothesis testing; statistical inference for two samples; analysis of variance; linear and non-linear regression; design of experiments; factorial experiments.
CH 299 32:0 - Dissertation Project
The project is aimed at training the students to analyze independently any problem posed to them. The project may be theoretical, experimental, or a combination of the two. In few cases, the project may also involve sophisticated design work. The project report is expected to show clarity of thought and expression, critical appreciation of the existing literature, and analytical, experimental or design skills.
CH 232 (JAN) 1:0 - Physics of Fluids
Classical mechanics: Lagrangian and Hamiltonian formulations, Liouville equation and BBKGY hierarchy. Kinetic theory of gases: Velocity distribution function and analysis of collisions, Boltzmann equation and Boltzmann H – Theorem, Nonequilibrium transport properties, Derivation of Navier-Stokes equations, Theory of dense gases. Stochastic processes: Brownian motion, Central limit theorem, Markov processes, Fokker Planck and Langevin equations. Linear response theory: Space-time correlation functions, Response functions, Fluctuation-dissipation theorem, Generalized hydrodynamics: Generalized Navier-Stokes equations, Green – Kubo relations.
CH 234 (JAN) 3:0 - Rheology of Complex Fluids and Particulate Materials
Introduction to complex fluids: Polymeric fluids, suspensions, pastes, dry granular materials; Flow phenomena in complex fluids shear thinning and thickening, shear bands, creep; Introduction to principles of rheology; Kinematics viscometric flows; material functions: rheometry in simple flows; Rheological models Generalized Newtonian fluid, models for viscoelasticity, plasticity and viscoplasticity; Applications to simple flow problems.
CH 235 (AUG) 3:0 - Modeling in Chemical Engineering
Model development principles; classification of models; modeling of complex situations of interest to chemical engineers through lumped parameter models, continuum models, population balance models, stochastic models, Monte Carlo methods, network models, percolation concepts, and fractal analysis of complex geometries.
CH 236 (JAN) 3:0 - Statistical Thermodynamics
Macroscopic and microscopic descriptions of the state of a system.Ensembles, the partition function and thermodynamic properties; System of independent particles; Fluctuations andthe compressibility equation; Chemical equilibrium in ideal gas mixtures; Lattice statistics; Real gases; The liquid state: lattice models,distribution functions theories, perturbation theories; Liquid mixtures: solution theories and local composition models
CH 242 (AUG) 3:0 - Special Topics in Theoretical Biology
Motivation for theoretical studies of biological phenomena; reaction-diffusion systems; biological oscillations and chaotic systems; bacterial chemotaxis; interacting population dynamics; within-host dynamics of viral infections; virus-cell interactions; host immune response; drug pharmacokinetics and therapy; disease epidemiology; HIV and hepatitis C virus infections; tumor progression and cancer.
CH 243 (JAN) 3:0 - Mechanics of Particle Suspensions
Forces acting on particles in a fluid-particle suspension; Flow regimes; Creeping flow: Fundamentals of Stokes flow, singularity solutions, and the fluid velocity disturbance due to an isolated particle; Inertial flow: fluid-particle and particle-particle interactions; Hydrodynamic interactions between suspended participles; Sedimentation, rheology and self-diffusion of dilute Stokesian suspensions; Dynamics of concentrated suspensions; Continuum description of suspensions using volume and ensemble averaging; Non-linear rheology and segregation; Applications to living cells and other biological systems.
CH 245 (JAN) 3:0 - Interfacial and Colloidal Phenomena
Interfaces, Young-Laplace and Kelvin equations for curved interfaces; interfacial tension and contact angle, measurement techniques; wetting and spreading; intermolecular and interparticle forces, double layer repulsion, DLVO theory of colloidal stability; non-DLVO forces; surfactants; thermodynamics of self-assembly, phase diagrams; electro-kinetic phenomena, zeta potential; electrochemical systems.
CH 247 (JAN) 3:0 - Introduction to Molecular Simulations
Introduction to molecular dynamics; conservation laws; integration schemes: verlet, velocity verlet, leapfrog; constraint dynamics; extended Lagrangian dynamics; Thermostats and barostats; introduction to Monte Carlo techniques; Metropolis algorithm; NVT, NPT and GCMC simulations; estimation of pressure, chemical potential, radial distribution function, auto-correlation function, Ewald summation; umbrella sampling; Gibbs Ensemble technique; configuration bias technique.
CH 248 (JAN) 3:0 - Molecular Systems Biology
Various topics highlighting experimental techniques and modeling approaches in systems biology for problems ranging from molecular level to the multi-cellular level will be covered. Topics: Properties of biomolecules, Biomolecular Forces, Single molecule experimental techniques, Molecular motors, Molecular heterogeneity, Self-organization, Enzyme kinetics, modeling cellular reactions and processes, Fluctuations and noise in biology, Cellular variability, Biological networks, Modeling dynamics of bioprocesses and Cellular signaling.
Course Notes:
The course is intended for Masters and PhD students. Undergraduates with sufficient background may approach the instructor regarding the course.
No prior knowledge of biology is needed but a non-biologist will have to self-educate.
Basic grasp of calculus, algebra and programming skills in C, Matlab or Mathematica is recommended.
CH 249 (JAN) 3:0 - Structural and Functional DNA Nanotechnology
Origin of structural DNA nanotechnology; properties of DNA and other nucleic acids relevant to nanotechnology; design of branched DNA systems; DNA nanomechanical devices; DNA origami and DNA bricks; Forces and energetics in nanoscale; Thermodynamics of self-assembly formation; Experimental techniques to characterize DNA nanostructures including AFM; SEM; TEM; single molecule and bulk fluorescence; gel electrophoresis; sequencing and radio-labelling assays; Application of DNA nanostructures in molecular computing; organizing and templating other nanomaterials; bio-sensing; nano-fabrication; cargo delivery; hybrid DNA nanomaterials.
CH 251 (JAN) 3:0 - Machine Learning for Materials and Molecules
Introduction to data science and machine learning, examples of supervised/unsupervised/reinforcement learning, motivation behind modeling materials and molecules with examples from sustainable energy conversion and storage, clean water/air, and human health; introduction to Python, scientific computing packages (NumPy, SciPy, Matplotlib), and simple ML packages (Scikit-learn, RDKit, DeepChem); linear and nonlinear regression, confidence intervals and goodness of fit, loss functions, gradient descent algorithm, overfitting/underfitting, regression/classification learning; clustering, singular-value decomposition, and principal component analysis; decision trees and ensemble methods, random forests, boosting and bagging techniques, gradient-boosted machine learning, hyperparameter tuning; introduction to neural networks and deep learning; basics of data generation using molecular dynamics, Monte Carlo, and density functional theory simulations; cheminformatics, graph and featurized representations of materials, molecules, and nanopores, and their applications in materials/molecular discovery; introduction to neural network potentials; application of machine learning in predicting molecular/materials properties
CH 254 (JAN) 3:0 - Heterogeneous Catalysis for Environmental Remediation
Overview of inorganic and organic contaminants in water, permissible limits and effects; introduction to primary, secondary and tertiary water treatment processes; fundamentals of heterogeneous catalysis; steps of catalytic reactions: rate-determining steps and rate equations, effectiveness factors; overview of advanced oxidation process; homogeneous and heterogenous Fenton processes: photocatalysis, piezo-catalysis, photothermal catalysis, electro-Fenton process; design, preparation, characterization and modulation of heterogeneous catalysts; degradation and transformation of contaminants; effects of various parameters on catalytic contaminant removal; scalability and practical applications of heterogeneous catalysts.